详解桶排序以及排序总结

堆

堆结构就是用数组实现的完全二叉树结构

完全二叉树中如果每棵子树的最大值都在顶端就是大根堆

完全二叉树中如果每棵子树的最小值都在顶端就是小根堆

堆结构的heapInsert与heapify操作

堆结构的增大和减少

优先级队列结构，就是堆结构

首先要了解什么是完全二叉树？

完全二叉树是由满二叉树而引出来的，若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数(即1~h-1层为一个满二叉树)，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

我们可以用数组来表示，从0开始的连续一段看作是完成全二叉树，用size来规定有几个数是这个树里。

他具有以下特性：

i位置的左孩子可以表示为： $2 \times i +1$

右孩子： $2 \times i +2$

父： $\frac{i-1}{2}$

而堆是比较特殊的完全二叉树，所谓大根堆表示每一颗子树的最大值都是头节点的值，反之则是小根堆。

堆排序

在进行堆排序之前，让我们先引入heapInsert和heapify操作：

heapInsert操作

以大根堆为例：

在算法中，我们可以先堆再比较，在插入一个数字时与他的父节点（ $\frac{i-1}{2}$ ）比较，如果比他大的话就进行交换，如果交换后之后父节点还是小，那么再交换，也就是一直跟自己的父节点比较，什么时候来到头位置或者不再大，那么停止。这个插入的过程可以叫做heapinsert。同时还会有其他操作，比如告诉用户给的数字中最大的数字，同时拿掉这个数字，并且在这之后仍然成堆结构。

public static void heapInsert(int[] arr ,int index){
    while(arr[index] > arr[(index - 1)/2]){
        swap(arr , index , arr[(index - 1)/2]);
        index = (index - 1)/2;
    }
}

heapify操作

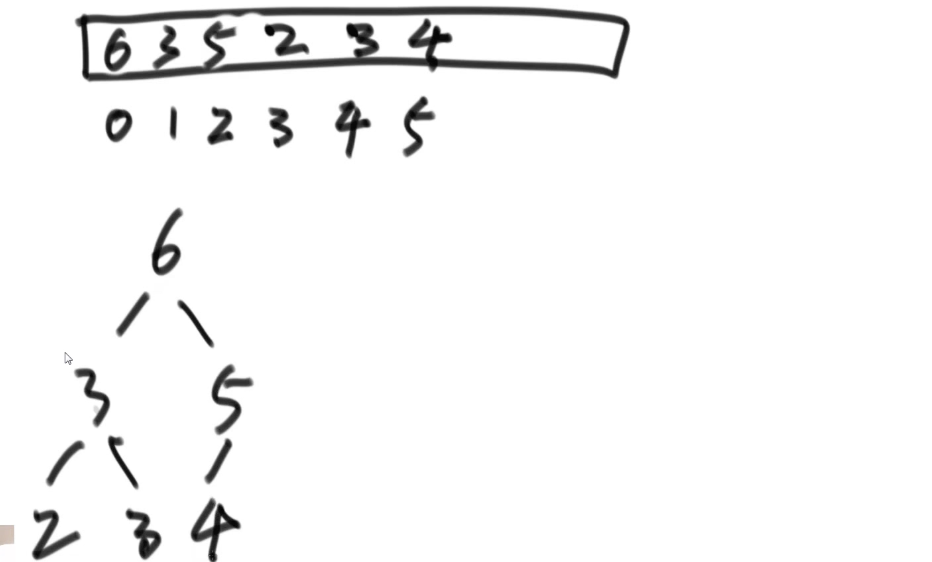
以该图为例，heapSize=6，现在我们知道在第0个位置上就是当前最大的数字，我们先把这个数字用一个临时变量存储，记录下来，这时候把已经形成的堆结构的最后一个数字，也就是4，放在0位置上，同时heaoSize—，这时候arr[5]已经无效越界了，不再是堆的内容。但这时候整体可能就不再是堆。这时候我们从头节点开始，先在他的孩子中找一个最大值，并且进行比对，如果头节点比孩子小，那么交换，将这个“4”放下去。“5”放上去。停止的标志是不再有孩子或者不再小于孩子。这个过程叫heapify，堆化。

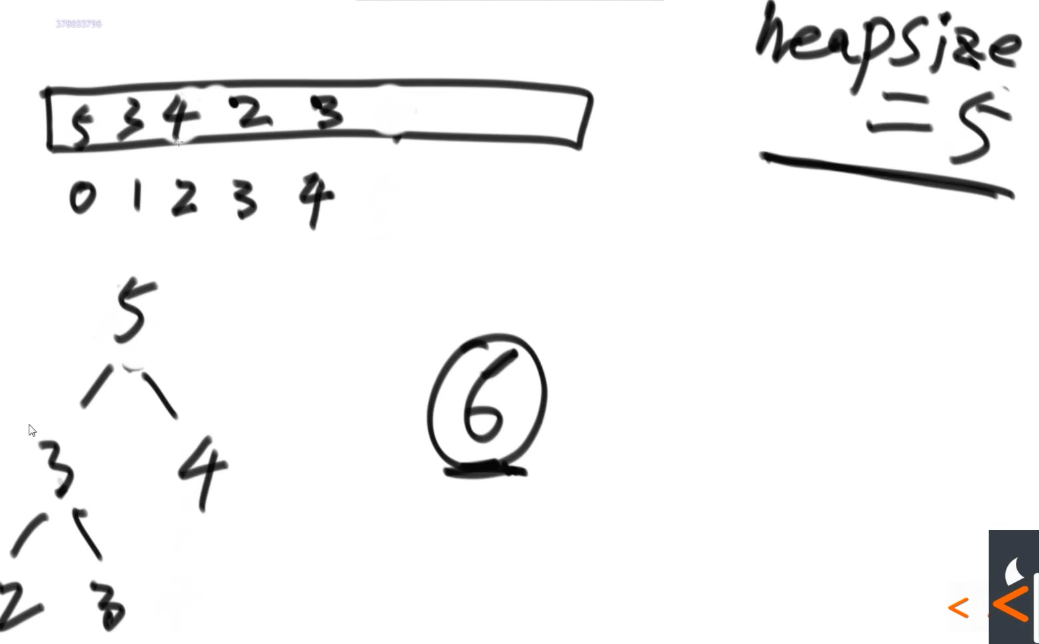
public static void heapify(int[] arr, int index, int heapSize){
    int left = index * 2 + 1;
    while(left < heapSize){
        int largest = left + 1 <heapSize && arr[left+1] > arr[left] ? left + 1 : left;
        largest = arr[largest] > arr[index] ? largest : index;
        if(largest == index){
            break;
        }
        swap(arr , index ,largest);
        index = largest;
        left = index * 2 + 1;
    }

}

这句判断什么时候右孩子可以放largest，首先右孩子要存在，并且比左孩子大，那么这个时候再将下标给largest。左孩子可以做最大值有两个可能，第一没有右孩子，第二右孩子比左孩子小，这一句包括了这两个判断。

1	int largest = left + 1 <heapSize && arr[left+1] > arr[left] ? left + 1 : left;

如果这之后largest的值就等于父节点的值，那就说明父节点就是最大值，不需要往下走，直接break，反之需要往下走。把largest和父做交换，index此时发生变化，并且有新的左孩子，继续走while判断，如果不再有孩子while停，有孩子但是孩子不比父亲大，break。

if(largest == index){
    break;
}
swap(arr , index ,largest);
index = largest;
left = index * 2 + 1;

时间复杂度分析

举个例子，此时已经排好了一个堆，但是用户想要将某个位置上的值换个数字，那么想要继续成堆，只需要判读这个数字和原数字谁大谁小。如果这个数字更大的话，那就执行heapInsert操作，将它往上放，反之，就执行heapify操作，将下面的部分调整成堆结构。

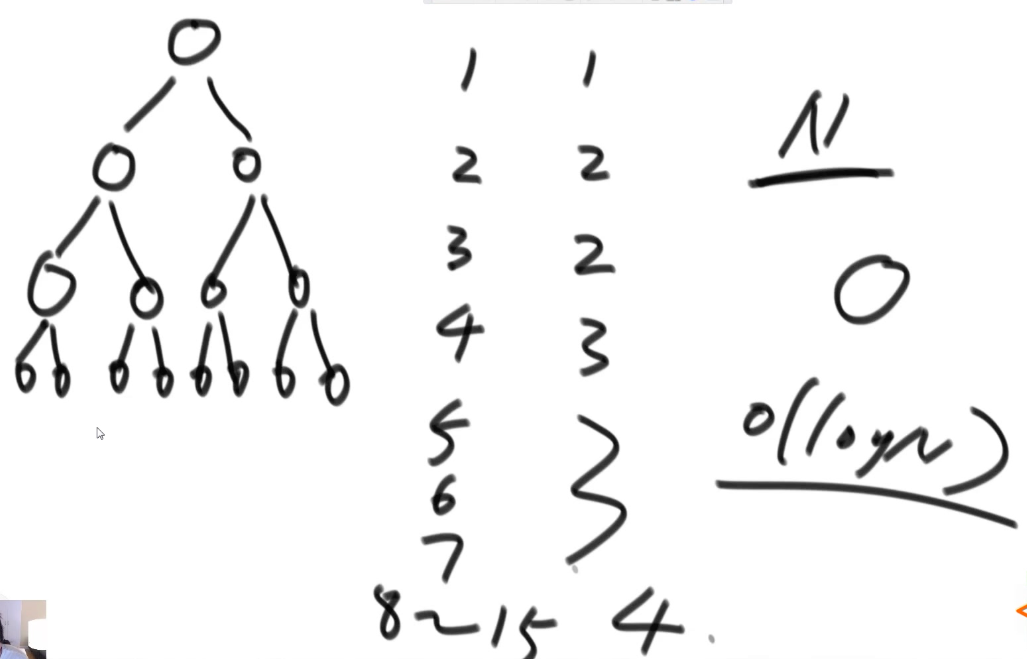
在这张图中我们可以明显看到，完全二叉树的高度与有多少的节点的关系，所以是 $O(logN)$ 级别。而heapInsert操作，只需要关注父这一条路径上去，只跟高度有关，所以是 $logN$ 级别的。用户删掉最大值并且让之后继续成堆，还是往下走一条高度，所以也是 $logN$ 级别的调整代价。

接下来我们正式进入堆排序的过程：

先让整个数组都变成大根堆结构，建立堆的过程：
(1). 从上到下的方法，时间复杂度为 $O(N \times logN)$
(2). 从下到上的方法，时间复杂度为 $O(N)$

把堆的最大值和堆末尾的值交换，然后减少堆的大小之后，再去调整堆，一直周而复始，时间复杂度为 $O(N \times logN)$

把堆的大小减少成0之后，排序完成

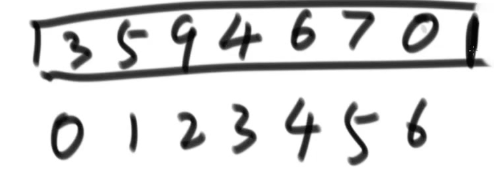
先让0～0范围上是堆，很显然已经是，接着是0～1，0～2，在这时，5和3需要交换，9要跟我交换，heapSize在变大。4进来需要跟3交换，6跟4交换，7跟5交换，0不用动。现在整个都是大根堆。（这是一个heapInsert过程。）

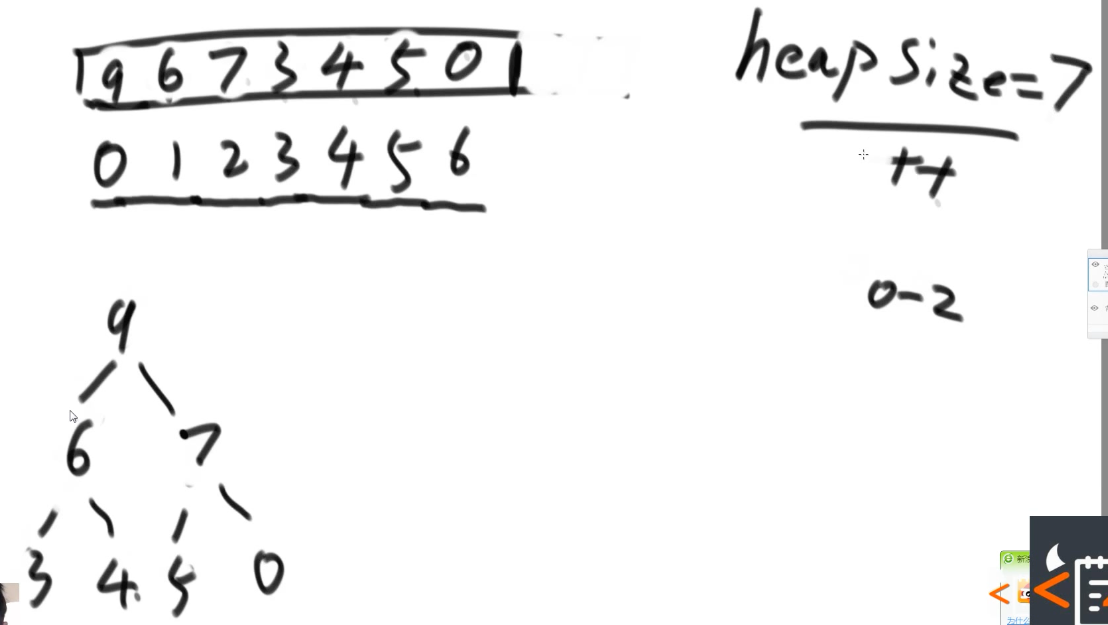
接着把0位置上的9和6位置上的0做交换（最大值和堆上最后一个位置做交换），heapSize—变成6，即把最后的位置跟堆断开了。 9断开。

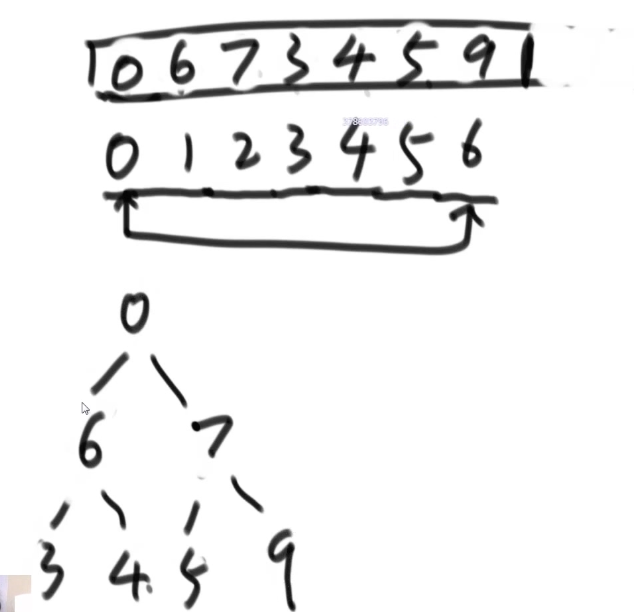
然后从0位置上的0做heapify，让剩下的部分继续成堆结构。

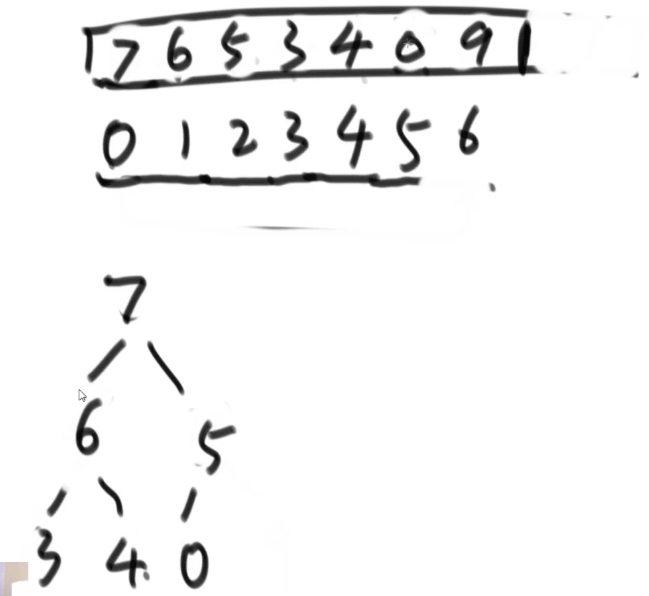
接着继续做交换，把最大与堆末尾交换，然后7断开。周而复始……

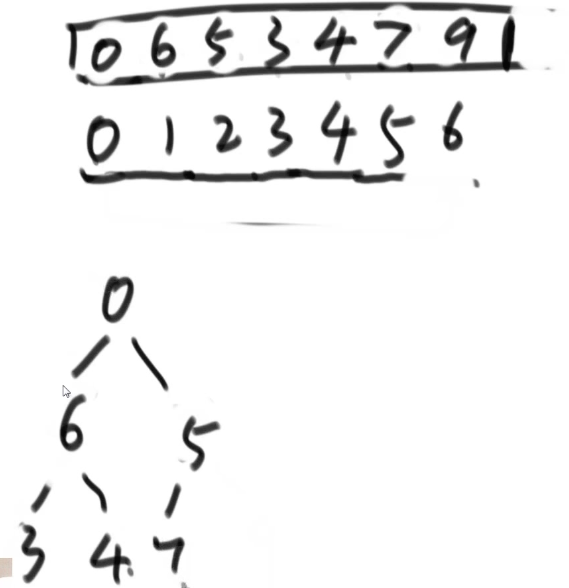
public static void heapSort(int[] arr){
    if(arr == null || arr.length < 2){
        return;
    }
    for(int i =0; i < arr.length; i++){
        heapInsert(arr , i);
    }
    int heapSize = arr.length;
    swap(arr , 0 , --heapSize);
    while (heapSize > 0){
        heapify(arr , 0 ,heapSize);
        swap(arr , 0 , --heapSize);
    }
}

这一步将整体变成大根堆：

1
2
3

for(int i =0; i < arr.length; i++){  //O(n)
    heapInsert(arr , i);  //O(logN)
}

然后和堆上最后一个位置的数做交换，堆大小减1：

1	swap(arr , 0 , --heapSize);

只要heapSize大小没减成0就继续周而复始。

while (heapSize > 0){  //O(n)
    heapify(arr , 0 ,heapSize);  //O(logN)
    swap(arr , 0 , --heapSize);  //O(1)
}

算法整体复杂度为O(NlogN)，同时额外空间复杂度为O(1)。

同时成大根堆的方法还可以从下往上：

//从下到上的成大根堆的方法，时间复杂度为O(N)
for(int i = arr.length -1 ; i >= 0 ; i--){
    heapify(arr , i , arr.length);
}

最底下一层有 $\frac{N}{2}$ 个节点，倒数第二层 $\frac{N}{4}$ …这样一层一层的进行堆化操作，也可以成大根堆。时间复杂度为O(N)。

在最下面一层，几乎什么都不用干，所以时间复杂度为O(1)，往上一层的堆化则是需要1层的操作…

$T(N) = \frac{N}{2} \times 1 + \frac{N}{4} \times 2 + \frac{N}{8} \times 3 + \frac{N}{16} \times 4 + ...$ $2T(N) = \frac{N}{2} \times 2 + \frac{N}{2} \times 2 + \frac{N}{4} \times 3 + \frac{N}{8} \times 4 + ...$

得到：

$T(N) = N +\frac{N}{2} + \frac{N}{4} + \frac{N}{8} + ...$$ ，后面是个等比数列求和，最终结果就是O(N)。 ### 堆排序的拓展题目 > 已知一个几乎有序的数组，几乎有序是指，如果把数组排好顺序的话，每个元素的移动的距离可以不超过k，并且k相对于数组来说比较小。请选择一个合适的排序算法对这个数据进行排序。意思就是说数字所在的位置和他排完序应该在的位置不超过k。举例说明，假设k=6，准备一个小根堆（一个结构），然后遍历数组，先遍历前7个数，下标从0～6的七个数字扔到小根堆里，小根堆的最小值一定在0位置，将小根堆的最小值弹出，拿着这个数字放在0位置上，接着像滑动一样周而复始，最后数组临近结束时，只要依次将小根堆的最小数弹出，整个数组就几乎有序了。复杂度是$$O(NlogK)$

小根堆在Java中可以直接用优先级队列（堆结构，不加参数就是小根堆）表示：

1	PriorityQueue<Integer> heap = new PriorityQueue<>();

先把前k个数放到小根堆：

int index = 0;
//先把前k个数放到小根堆
for( ; index <= Math.min(arr.length, k) ; index++){
    heap.add(arr[index]);
}

加一个弹一个：

int i = 0;
for( ; index < arr.length ; i++ , index++){
    heap.add(arr[index]);
    arr[i] = heap.poll();
}
while (!heap.isEmpty()){
    arr[i++] = heap.poll();
}

比较器

比较器的实质就是重载比较运算符

比较器可以很好的应用在特殊标准的排序上

比较器可以很好的应用在根据特殊标准排序的结构上

其实Java中的比较器就相当于C++中的重载比较运算符。

例如自己定义的一个Student，如果用系统自带的，只会比较无意义的内存地址。

通过控制返回值我们可以确定如何排序，所有的比较器的潜台词：返回负数的时候，第一个参数排在前面，返回正数的时候第二个参数排在前面，返回0谁在前面无所谓。那么对于堆结构，其实就相当于如果返回负数，第一个参数放在上面，返回正数则是第二个参数放在上面。

举个例子，在下面的代码中，如果o1的id小，返回的就是负数，o1就放前面，如果o2的id小，返回的就是负数，那么o2放前面。

public static class IdAscendComparator implements Comparator<Student>{
        //返回负数的时候，第一个参数排在前面
        //返回正数的时候，第二个参数排在前面
        //返回0的时候谁在前面无所谓
        @Override
        public int compare(Student o1 , Student o2){
//            return o1.id-o2.id;
            if(o1.id < o2.id){
                return -1;
            }
            if(o2.id < o1.id){
                return 1;
            }
            return 0;
        }
    }

该行代码表示的是，用你给的IdAscendingComparator方法去排序students：

1	Arrays.sort(students,new IdAscendComparator());

桶排序思想下的排序

桶排序思想下的排序都是不基于比较大排序

时间复杂度为O(N)，额外空间复杂度O(M)

应用范围有限，需要样本的数据状况满足桶的划分

计数排序

举个例子，现在需要对某公司的员工的年龄进行排序。在前面所有的排序都是基于比较得出的结论，而对于年龄来说，我们知道打工人的年龄在[16,200]之间，那么我们就可以定义一个数组，int age[]，数组的下标表示年龄，存放的数据表示遍历过整个公司的员工后等于下标年龄的员工的个数，这样一来就很容易再将其还原。

基数排序

以下图为例

IMG_C7023536AE94-1

先根据个位数字排序，接着是十位，百位，百位是最后放桶里，所以优先级最高。而十进制是第二高优先级，个位也将优先级保留下来了。十进制数字使用十个桶，同理八进制就用八个桶。这也是根据数据状况产生的排序。

在数组[L~R]范围上要排序，digit代表这批数字中最大的值有几个十进制位。maxbits就是寻找最大值有多少位。getDigit是获取dight。

IMG_E9A019B4FE24-1

public class Code02_RadixSort {

    //only for no-negative value
    public static void radisSort(int[] arr){
        if(arr == null || arr.length < 2){
            return;
        }
        radixSort(arr,0,arr.length-1,maxbits(arr));
    }

    public static int maxbits(int[] arr){
        int max = Integer.MIN_VALUE;
        for(int i = 0; i < arr.length ; i++){
            max = Math.max(max,arr[i]);
        }
        int res = 0;
        while (max != 0){
            res++;
            max /= 10;
        }
        return res;
    }

    //arr[begin...end]排序
    public static void radixSort(int[] arr, int L, int R, int dight){
        //以10为基底
        final int radix = 10;
        int i = 0,j = 0;
        //有多少个数准备多少个辅助空间
        int[] bucket = new int[R-L+1];
        /*
        有多少位就进出几次：代表出桶入桶多少次，跟位数有关（最大的for循环的意思）
        十个空间
        count[0]  当前位(d位)是0的数字有多少个
        count[1]  当前位(d位)是(0和1)的数字有多少个
        count[2]  当前位(d位)是(0,1,3)的数字有多少个
        count[i]  当前位(d位)是(0~i)的数字有多少个
         */
        for(int d = 1; d <= dight; d++){
            int[] count = new int[radix];
            for(i = L; i <= R; i++){
                j = getDight(arr[i],d);
                count[j]++;
            }
            for(i = 1; i < radix; i++){
                count[i] = count[i] + count[i-1];
            }
            for(i = R; i >= L; i--){
                j = getDight(arr[i],d);
                bucket[count[j]-1] = arr[i];
                count[j]--;
            }
            for(i = L, j = 0; i <= R; i++, j++){
                arr[i] = bucket[j];
            }
        }
    }

    public static int getDight(int x, int d){
        return ((x / ((int)Math.pow(10,d-1)))%10);
    }
}

getDight

getDight(int x, int d)中x代表传入的数字，d代表判断x的个位/十位/百位，返回值即为x的d位数。其中Math.pow(x,y)中x代表底数，y代表幂，整体代表 $x^y$ ，我们知道求一个数字各个位数上的值可以用除法取模来计算。比如123想得到第十位上的值，首先就是将位数取成两位数，只需要除以一个十，即 $123 \div 10 =12$ （在计算机中整数除以整数会损失精度，得到的还是整数），再取模即可得到最后一位数的值。同理1234取百位是除以两个十…

1
2
3

public static int getDight(int x, int d){
    return ((x / ((int)Math.pow(10,d-1)))%10);
}

maxbits

maxbits求的是最大的数是几位数。

public static int maxbits(int[] arr){
    int max = Integer.MIN_VALUE;
    for(int i = 0; i < arr.length ; i++){
        max = Math.max(max,arr[i]);
    }
    int res = 0;
    while (max != 0){
        res++;
        max /= 10;
    }
    return res;
}

radixSort

这里的大循环是从个位开始，逐个放进桶里。

for(int d = 1; d <= dight; d++){
    int[] count = new int[radix];
    for(i = L; i <= R; i++){
        j = getDight(arr[i],d);
        count[j]++;
    }
    for(i = 1; i < radix; i++){
        count[i] = count[i] + count[i-1];
    }
    for(i = R; i >= L; i--){
        j = getDight(arr[i],d);
        bucket[count[j]-1] = arr[i];
        count[j]--;
    }
    for(i = L, j = 0; i <= R; i++, j++){
        arr[i] = bucket[j];
    }
}

count数组的形成

for(i = L; i <= R; i++){
    j = getDight(arr[i],d);
    count[j]++;
}
//优化成前缀和形式
for(i = 1; i < radix; i++){
    count[i] = count[i] + count[i-1];
}

入桶出桶

从右往左遍历，bucket数组是辅助数组，在被赋值的同时count[j]递减。

for(i = R; i >= L; i--){
    j = getDight(arr[i],d);
    bucket[count[j]-1] = arr[i];
    count[j]--;
}

然后排序赋值

1
2
3

for(i = L, j = 0; i <= R; i++, j++){
    arr[i] = bucket[j];
}