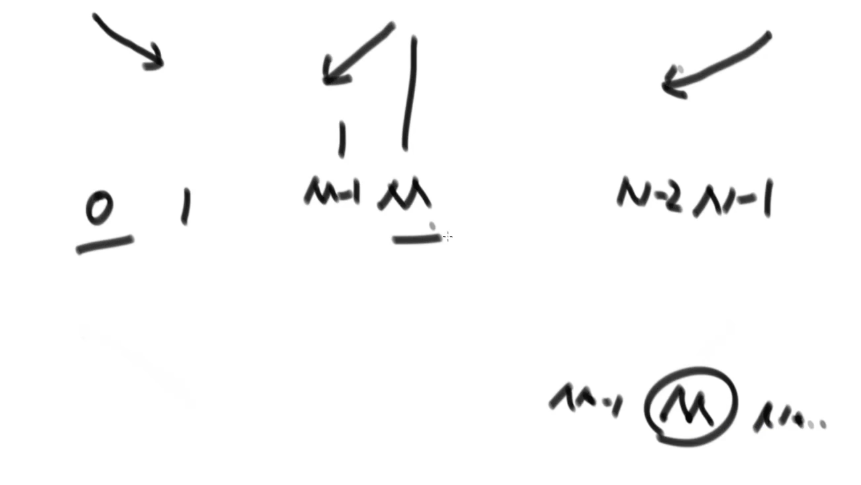本笔记内容均来源于左程云老师课程

一周刷爆Leetcode

认识复杂度和简单排序算法

时间复杂度

一般采用大O表示法，同时省去常数项

时间复杂度是一个算法流程中，常熟操作数量的一个指标，常用O表示。在表达式中过，只需要高阶项，不需要低阶项，也不需要高阶项大系数，剩下的部分如果为f(n)，那么时间复杂度即为O(f(n))。

评价一个算法流程的好坏，先看时间复杂度的指标，再分析不同数据样本在的实际运行时间，也就是“常数项时间”

常数操作

一个操作如果与样本的数据量没有关系，每次都是固定时间内完成的操作叫做常数操作。

简单排序算法

选择排序法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class SelcetionSort {
    public void selectionSort(int[] array){
        if(array == null || array.length<=2){
            return;
        }
        for(int i = 0; i < array.length; i++){
            /*选择排序的思想就是：
            首先从0到n-1之间选出最小的数字，并将其放在首位
            接着继续从1到n-1之间继续选择，直到选到最后
            minIndex代表选出的下标
             */
            int minIndex = i;
            for(int j = i+1;j < array.length; j++){
                //这一步其实就是双重循环进行选择
                minIndex = array[minIndex] > array[j] ? j : minIndex;
            }
            swap(i,minIndex,array);
        }

    }
    public static void swap(int i, int j , int[] arr){
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

在此过程中，开辟了变量i，变量j，且minIndex还会释放，那么空间复杂度为O(1)。

冒泡排序

这里用谁大谁往右移动的思想，首先是从第0个位置到第n-1个位置（搞定了最后一个位置，把最大的数字放到了最右边），接着循环往次，从第0个位置到第n-2个位置。那么相对应的，也可以是比较出最小的往左边移动，只不过循环的方式需要改变，就是从第0到n-1变为第1到n-1往次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class BubbleSort {
    public static void bubbleSort(int[] arr){
        if(arr.length < 2 ||arr == null){
            return;
        }
        for(int i = arr.length-1 ; i > 0 ; i--){
            for(int j = 0 ; j < i; j++){
                /*
                从第0号下标开始，向最后一个来寻找最大第值放到最右边，
                多重循环先从最里面开始看，那么这里代表的就是从0到n-1再从0到n-2
                 */
                if(arr[j] > arr[j+1]) {
                    swap(arr,j,j+1);
                }
            }
        }
    }

    //交换arr的i和j位置上的值
    public static void swap(int[] arr ,int i ,int j){
        arr[i] = arr[i] ^ arr[j];
        arr[j] = arr[i] ^ arr[j];
        arr[i] = arr[i] ^ arr[j];
    }
}

补充：异或操作

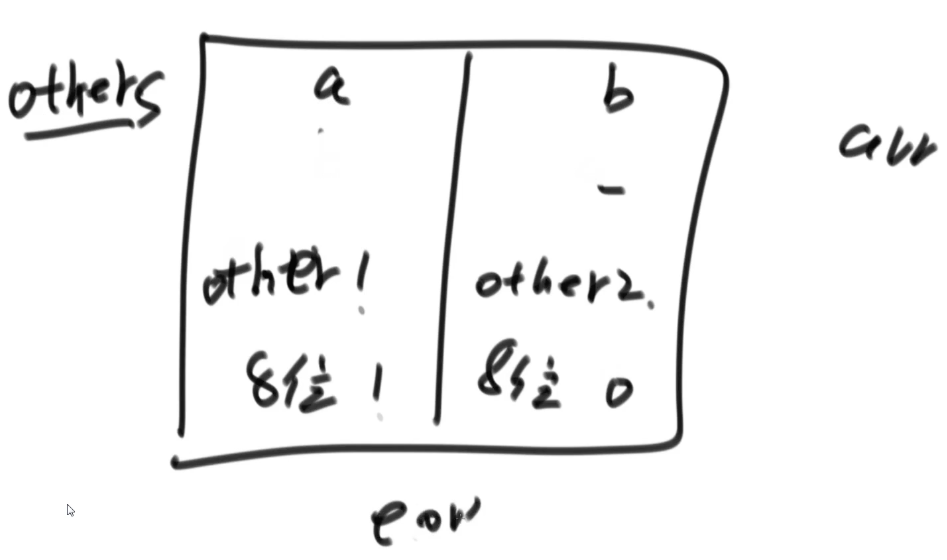
相同为0，不同为1。举例：a:10110;b:00111 ，那么a^b的结果就是10001 。同时异或操作还可以理解为无进位相加

性质：

  • 0^n=n
  • n^n=0
  • 异或运算满足交换律和结合律
  • 同一批数字异或的结果相同（例如二进制数字无进位相加，其结果其实只跟1出现的次数有关，这样可以解释为什么满足）

那么：假设int a =甲,int b = 乙

a=a^b; => a = 甲 ^ 乙 ，b = 乙

b=a^b; => a = 甲 ^ 乙 ，b= 甲 ^ 乙 ^乙，再根据交换律，乙 ^乙= 0 ，而甲 ^ 0 = 甲 =>b = 甲

a=a^b; => a = 甲 ^ 乙 ^ 甲 =乙， b = 甲

这三行代码的作用其实就是交换，但是能这么做的前提是a和b在内存里是两块独立的区域 ，即a可以等于b，值可以一样，但是必须保证a所指向的内存和b指向的内存不一样。如果相同内存地址，那么会被抹成0。

题目举例

（1）已知在一个数组中有一种数出现了奇数次，其他数都出现了偶数次，怎么找到这个数字

（2）..两种数字，找到这两个数字

要求时间复杂度为O(n)，空间复杂度为O(1)。

思路：

（1）偶数次的数字异或之后都会变成0，那么再结合异或操作的结合律和交换律，将整个数组与0异或就可以得到剩下的那个数字。

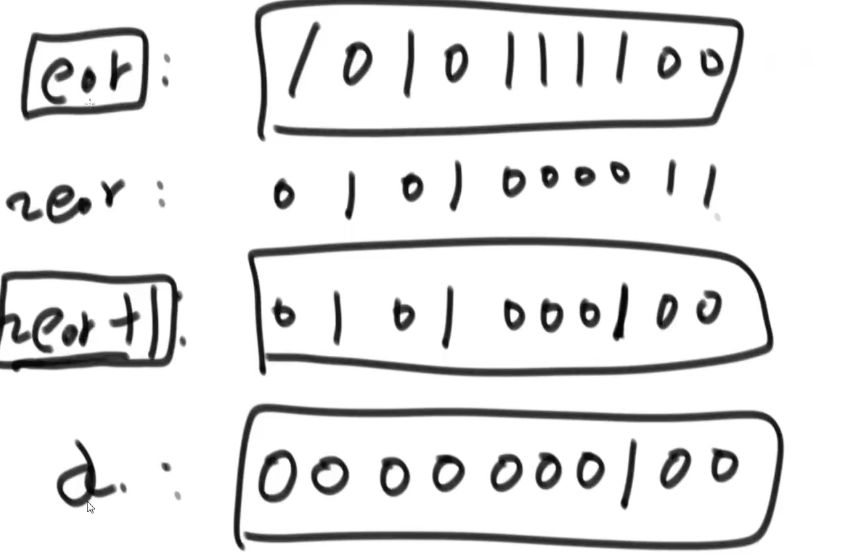
（2）不妨假设这两个数字是a和b，剩下其他的都是出现偶数次的，那么最后的结果一定是eor=a^b，且a不等于b，且eor不等于0。那么可以推断出eor一定至少有一位不为0，假设就在第八个位置上（整数一共32位），那么就说明a与b在第8个位置上不一样。那么再准备一个变量eor1，让整个数组的第八位上只为1的数再与eor1异或，a和b一定会分出来在两个集合中，一个是第八位为0的一个是第八位为1的。eor1=a or b。eor再与eor1异或就可以得到另一个。

image-20230306141859684

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public class Code01_EvenTimesOddTimes {
    public static void printOddTimesNum1(int[] arr){
        //已知在一个数组中有一种数出现了奇数次，其他数都出现了偶数次，怎么找到这个数字
        int eor = 0;
        for(int cur : arr){
            eor ^= cur;
        }
        System.out.println(eor);
    }

    public static void printOddTimesNum2(int[] arr){
        //已知在一个数组中有两种数出现了奇数次，其他数都出现了偶数次，怎么找到这两个数字
        int eor = 0 , eor1 = 0;
        for(int curNum : arr){
            eor ^= curNum;
        }
        /*
        eor = a ^ b;
        eor != 0
        eor必然至少有一个位置上是1
        RightOne是最右边为1 的
        在if判断的时候不管是1还是0都可以，只做分类
         */
        int RightOne = eor & (~eor + 1);
        for(int cur : arr){
            if((cur & RightOne) == 0){
                eor1 ^= cur;
            }
        }
        System.out.println(eor1 + " " + (eor ^ ero1));
    }
}

~eor是eor取反

示例图

插入排序

其时间复杂度是O(n^2)，空间复杂度O(1)。

先做到0-0范围上有序，然后是0-1，如果1位置上的数字比0位置小，那么换位置，从1往前看。同理在0-n上，从n往前看。类比于斗地主抓牌。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class InsertionSort {
    public static void insertionSort(int[] arr){
        if(arr.length < 2 ||arr == null){
            return;
        }
        //0-1是有序的，0-i想有序
        for(int i = 0; i < arr.length; i++){
            for(int j = i-1; j >= 0 &&arr[j]>arr[j+1]; j--){
                swap(arr,j,j+1);
            }
        }
    }
    public static void swap(int[] arr ,int i ,int j){
        arr[i] = arr[i] ^ arr[j];
        arr[j] = arr[i] ^ arr[j];
        arr[i] = arr[i] ^ arr[j];
    }
}

对于时间复杂度：数据状况不同时间复杂度按最差来看

二分法的详解与拓展

  1. 在一个有序数组中，找某个数是否存在:一半一半的范围找，一次砍一半的范围。时间复杂度是O(logn)

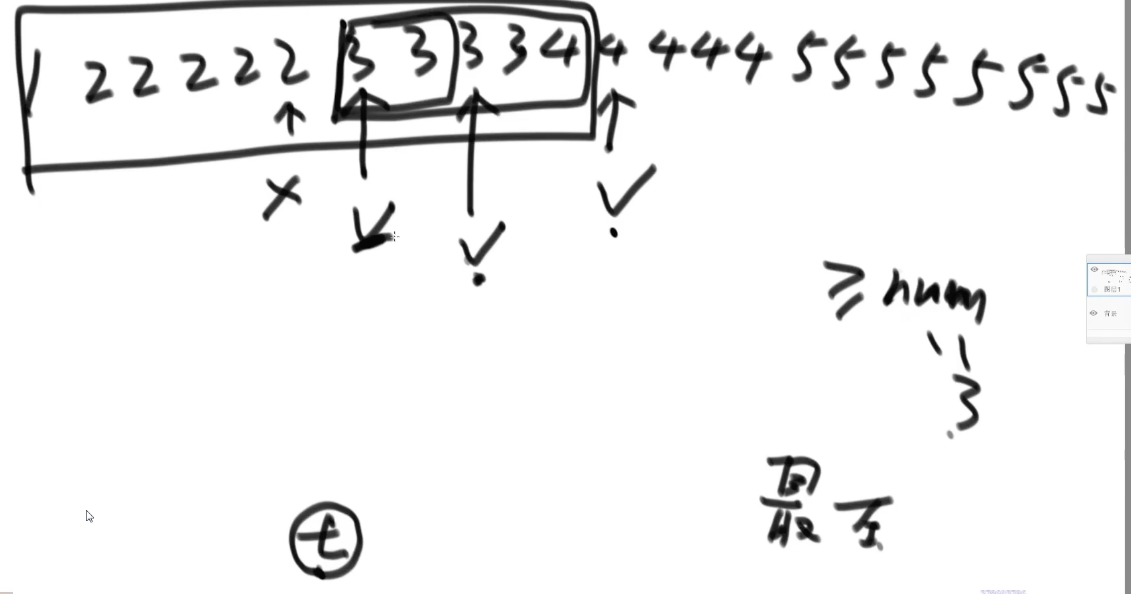
  2. 在一个有序数组中，找>=某个数最左侧的位置

  3. 局部最小值的问题，arr无序，但是任何两个相邻的数字不相等

可以用二分的思维（类似于连续函数介值定理）

对数器的概念和使用

  1. 有一个你想要测的方法a
  2. 时间复杂度不好但是容易实现的方法b
  3. 实现一个随机样本产生器
  4. 把方法a和方法b爬相同的随机样本，看看得到结果是否一样
  5. 如果有一个随机样本使得比对结果不一致，打印样本进行人工干预，改对方法a或者b
  6. 当样本数量很多时对比测试依然正确，可以确定方法a以及正确
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
import java.util.Arrays;

public class InsertionSort {
    public static void insertionSort(int[] arr){
        if(arr.length < 2 ||arr == null){
            return;
        }
        //0-1是有序的，0-i想有序
        for(int i = 0; i < arr.length; i++){
            for(int j = i-1; j >= 0 &&arr[j]>arr[j+1]; j--){
                swap(arr,j,j+1);
            }
        }
    }
    public static void swap(int[] arr ,int i ,int j){
        arr[i] = arr[i] ^ arr[j];
        arr[j] = arr[i] ^ arr[j];
        arr[i] = arr[i] ^ arr[j];
    }

    public static void compataror(int[] arr){
        Arrays.sort(arr);  //系统提供的排序，当作对数器的方法B
    }

    //for test
    public static int[] generateRandomArray(int maxSize,int maxValue){
        //Math.random(): [0,1）之间的所有小数，等概率随机返回一个
        //Math.random*N: [0,N)之间的所有小数，等概率随机返回一个
        //int(Math.random*N):[0,N-1)之间的所有整数，等概率随机返回一个
        int arr[] = new int[((int)((maxSize+1)*Math.random()))];  //长度随机
        for(int i = 0; i < arr.length; i++){
            arr[i] = (int)((maxValue+1)*Math.random())-(int)((maxValue)*Math.random());

        }
        return arr;
    }

    //for test
    public static int[] copyArray(int[] arr){
        if(arr == null){
            return null;
        }
        int[] res = new int[arr.length];
        for(int i = 0; i < arr.length; i++){
            res[i] = arr[i];
        }
        return res;
    }

    //for test
    public static boolean isEuqul(int[] arr1,int[] arr2){
        if((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)){
            return false;
        }
        if(arr1 == null && arr2 == null){
            return true;
        }
        for(int i = 0; i < arr1.length; i++){
            if(arr1[i] != arr2[i]){
                return false;
            }
        }
        return true;
    }
    //for test
    public static void printArray(int[] arr){
        if(arr == null){
            return;
        }
        for (int i:arr
             ) {
            System.out.print(i+" ");
        }
        System.out.println();
    }

    //for test
    public static void main(String[] args) {
        int testTime = 500000;
        int maxSize = 100;
        int maxValue = 100;
        boolean succeed = true;
        for(int i = 0; i < testTime; i++){
            int[] arr1 = generateRandomArray(maxSize,maxValue);
            int[] arr2 = copyArray(arr1);
            insertionSort(arr1);
            compataror(arr2);
            if(!isEuqul(arr1,arr2)){
                succeed = false;
                break;
            }
        }
        System.out.println(succeed ? "Nice" : "Fucking fucked!");

    }

}