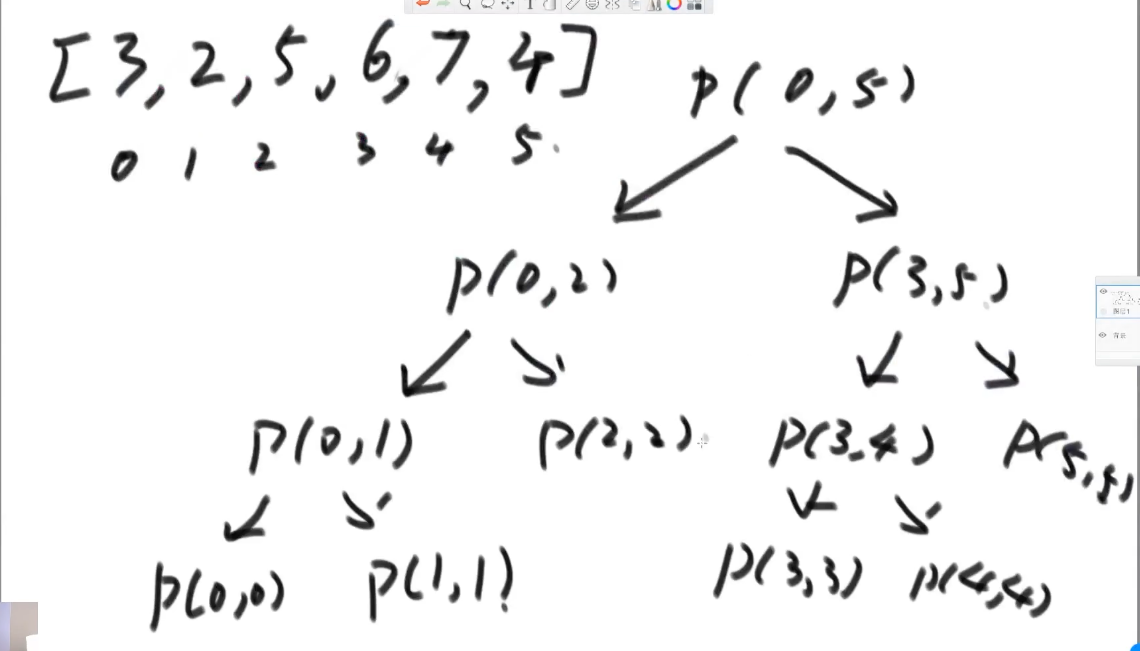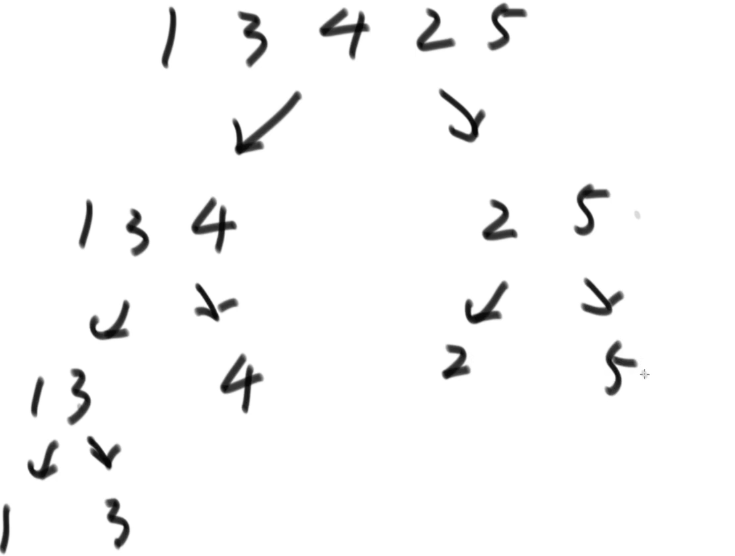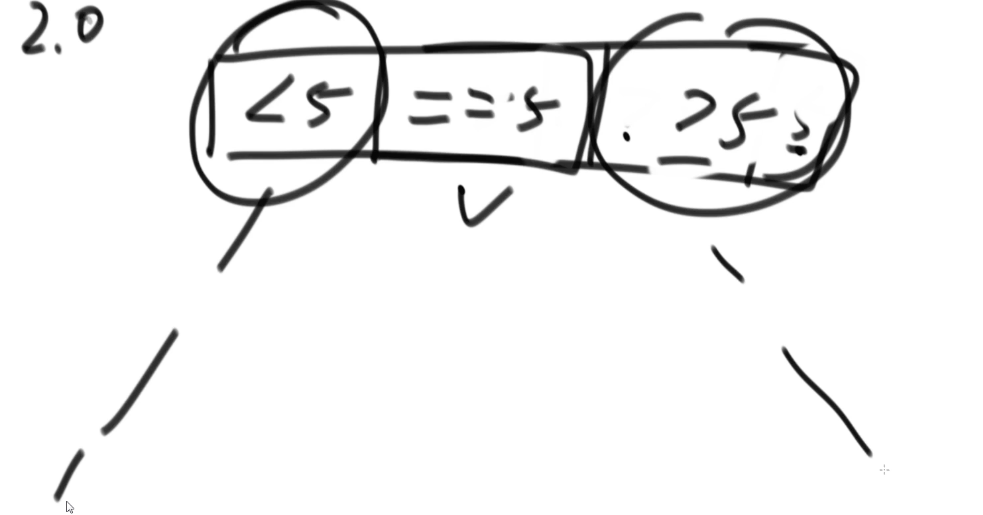认识O(NlogN)的排序
递归
首先有这样一个问题:我们在二分时喜欢用:
mid=(L+R)/2来表示,然而这么做却有一定的问题,L+R可能会溢出int的长度范围
所以可以写成:
mid=L+(R-L)/2;
再简化:mid = L + ((R- L))>> 1); 右移一位相当于除以二,左移相当于乘。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public class Code08_GetMax {
public static int getMax(int[] arr){
return process(arr,0,arr.length-1);
}
public static int process(int[] arr ,int L ,int R){
if(L == R){
return arr[L];
}
int mid = L + ((R-L) >> 1);
int leftMax = process(arr, L ,mid);
int rightMax = process(arr, mid+1 ,R);
return Math.max(leftMax,rightMax);
}
}
|
举例:比如有个数组[3,2,5,6,7,4];
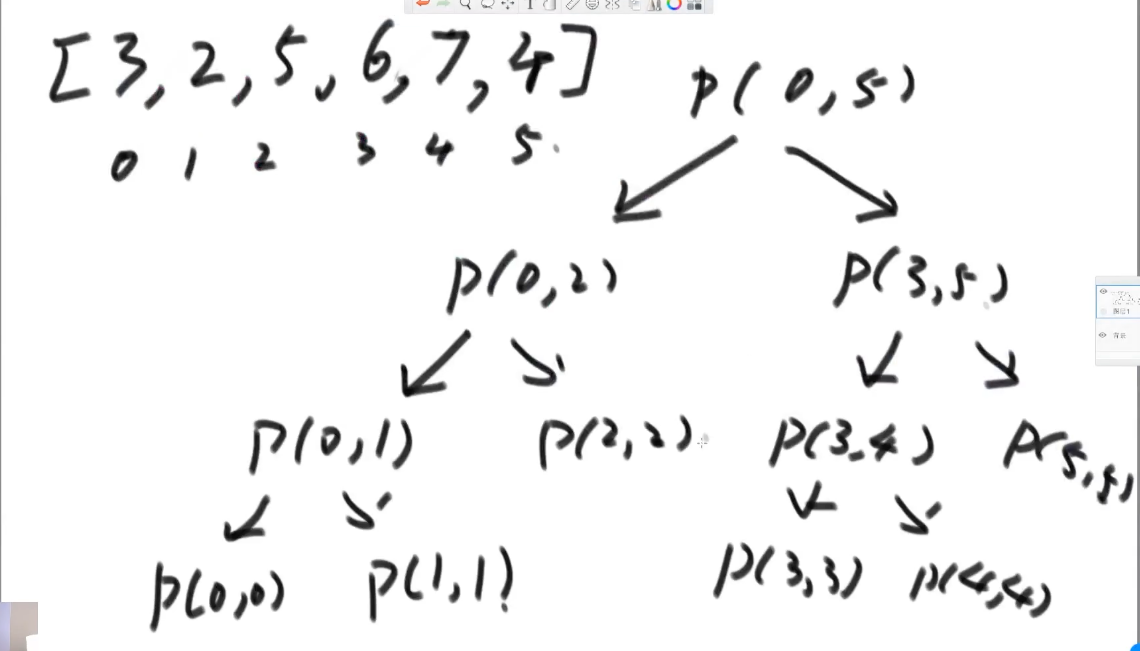
递归的过程其实就是压栈 (先进后出),执行p(0,5)的时候我们知道要先调p(0,2),所以p(0,5)进栈。这是一个后序遍历。
Master公式
T(N)指的是母问题的数据量是N,等号右边是函数里的细节。其中$T(\frac{N}{b})$代表每次的子过程的规模,a则代表子过程的调用次数,再后面是除了子过程之外剩下的过程的时间复杂度。
对于上面那行代码:
同时,一旦参数确定,时间复杂度即可确定
如果 时间复杂度为
如果 时间复杂度为
如果 时间复杂度为
归并排序
- 整体就是一个简单递归,左边排好序,右边排好序,让其整体有序
- 让其整体有序的过程里用了排外序方法
- 利用master公式求解时间复杂度i
- 归并排序的实质
时间复杂度,额外空间复杂度O(N)
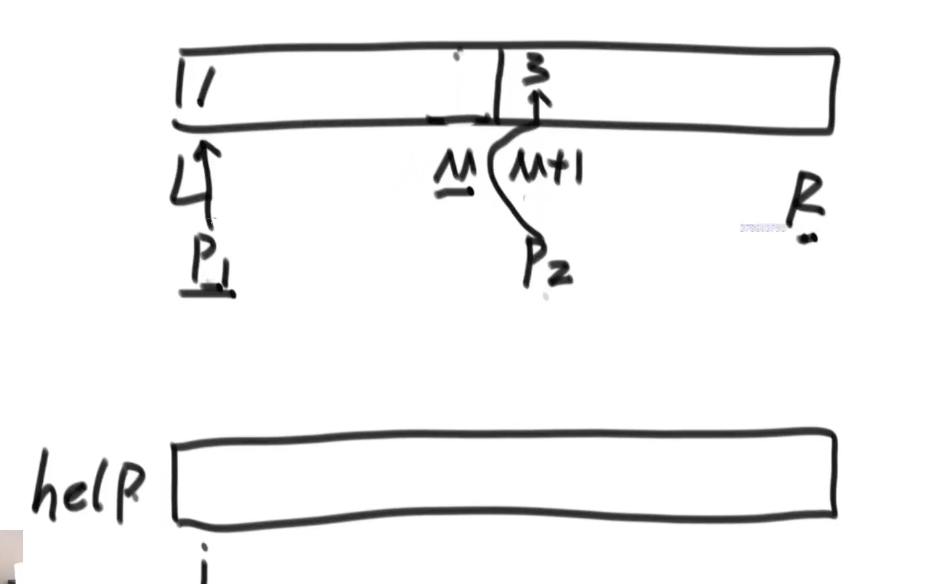
思路:想从L到R范围排好序,先把中点M分出左右,接着合并两个有序数组,使得合并的数组依然有序。
process是递归,先让左右都有序,再让整体有序。merge不是一个递归行为。
help是一个辅助空间,开辟的个数由L和R决定,跟原先数组等规模。
i是专门给help使用的一个变量。
p1是左侧部分的下标,p2是右侧部分下标。
首先判断是否越界,p1不超过M,p2不超过R,都不越界,谁小将谁拷贝到help里面,并且i也往下走。
但是总会有一个时刻会有越界,如果p1没越界,就把剩下的拷贝进去,两个while只会走一个。
再把help里的东西拷贝回原数组。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| public class MergeSort {
public static void mergeSort(int[] arr){
if(arr == null || arr.length < 2){
return;
}
process(arr,0,arr.length-1);
}
public static void process(int[] arr ,int L ,int R){
if(L == R){
return;
}
int mid = L + ((R-L) >> 1);
process(arr, L ,mid);
process(arr, mid+1 ,R);
merge(arr,L,mid,R);
}
public static void merge(int[] arr, int L, int R, int M){
int[] help = new int[R-L+1];
int i = 0;
int p1 = L;
int p2 = M+1;
while (p1 <= M && p2 <= R){
help[i++] = arr[p1] <= arr[p2] ? arr[p1++] :arr[p2++];
}
while(p1 <= M){
help[i++] = arr[p1++];
}
while (p2 <= R){
help[i++] = arr[p2++];
}
for(i = 0; i < help.length; i++){
arr[L + i] = help[i];
}
}
}
|
归并排序的拓展
小和问题
在一个数组中,每一个数左边比当前数小的数累加起来,叫做这个数组的小和。
例子:[1,3,4,2,5],1左边比1小的数没有;3左边比3小的数字:1;4左边比4小的数:1,3;2左边比2小的数:1;5左边比5小的数:1,3,4,2;所以小和为1+1+3+1+1+3+4+2=16
可以采用逆向思维的方法,对于1来说,右边比1大的有四个,就是说会有四个1,对于3来说,两个3,一个4,一个2。求一个数右边有多少个数比他大用归并排序很方便。
回想归并排序的过程,首先是分一半再分直到分到最后,那么这个过程中,在最底层逐渐弹栈时比较。
用以下图片举例:
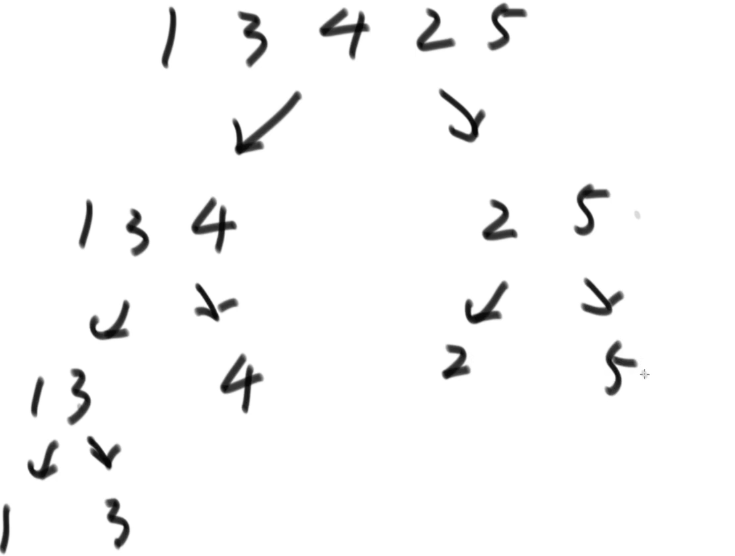
对于[1,3,4,2,5]这个数组,从最底下来看,一步一步merge:
首先是分成了[1,3],在这里面3在1右边比1大,有一个1。接着抹去最底下一层(递归弹出)merge成[1,3]。
数组变成了[[1,3],4],双指针,先从1看,左指针p1跟右指针p2=4比较,一个1;接着p1+1,3也比4小,一个3,然后左指针越界,将4拷贝下来merge成[1,3,4]。
然后问题来到整个数组的右侧,即[2,5]部分:左侧指向2,右侧指向5,拷贝的时候 左侧小产生一个2,然后左侧越界,右侧小的时候不产生小和,所以只产生了一个2.
然后[[1,3,4],[2,5]],左侧指针指向1,右侧指针指向2,可以看出左侧产生两个1, 然后左侧指向3,右侧有一个比3大,产生一个3,接下来是4,产生一个4,再越界,merge成[1.2.3.4.5]。
但是要注意,与归并排序不同的地方在于,求小和的时候当遇到两个数相等的时候需要将右侧的先拷贝。
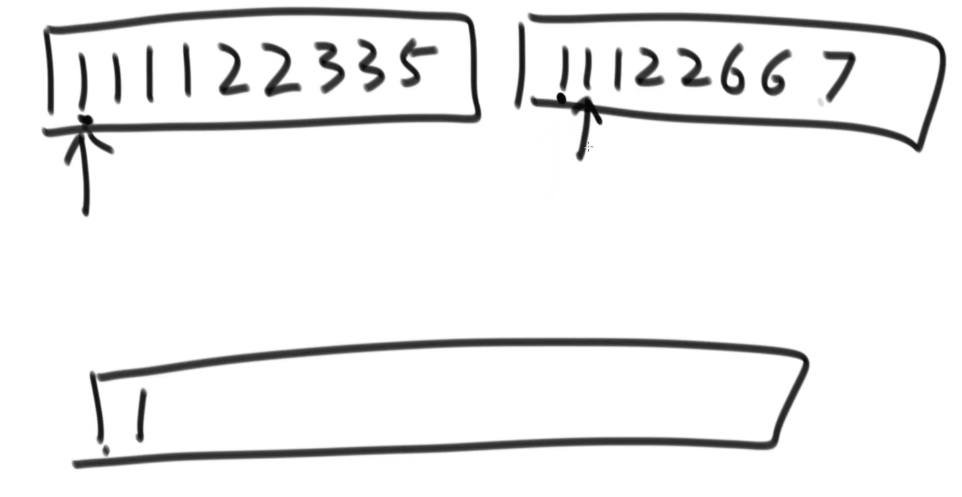
如上图所示:
第一个1和右侧指针指向的都是1,但是会先把右侧的拷贝下来,这样才能让指针继续向右走,才能继续看有多少个数比1大(注意,上图是已经走到最后一步的时候,两个数组已经排序好了)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| public class Code02_SmallNum {
public static int smallSum(int[] arr){
if(arr == null || arr.length < 2){
return 0;
}
return process(arr,0,arr.length-1);
}
public static int process(int[] arr ,int L ,int R){
if(L == R){
return 0;
}
int mid = L + ((R-L) >> 1);
return process(arr, L ,mid) +process(arr, mid+1 ,R) +merge(arr,L,mid,R);
}
public static int merge(int[] arr, int L, int R, int M){
int[] help = new int[R-L+1];
int i = 0;
int p1 = L;
int p2 = M+1;
int res = 0;
while (p1 <= M && p2 <= R){
res += arr[p1] < arr[p2] ? (R - p2 + 1) * arr[p1] : 0;
help[i++] = arr[p1] <=arr[p2] ? arr[p1++] :arr[p2++];
}
while(p1 <= M){
help[i++] = arr[p1++];
}
while (p2 <= R){
help[i++] = arr[p2++];
}
for(i = 0; i<help.length; i++){
arr[L + i] = help[i];
}
return res;
}
}
|
为什么可以做到不重不漏呢?
以数组中c举例:
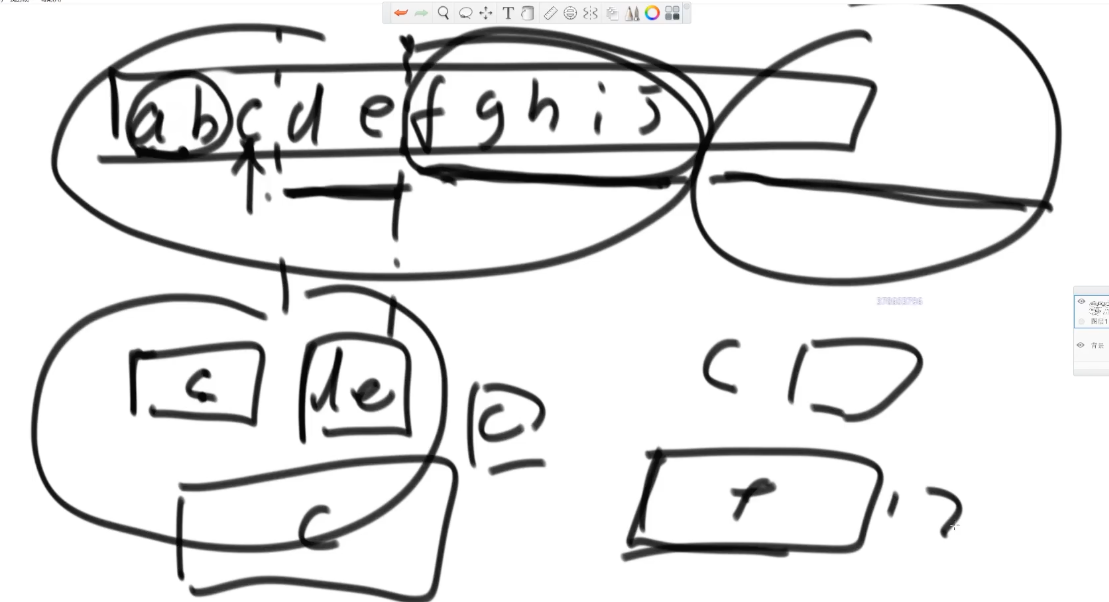
在形成这样一个数组之前,ab有序之前,肯定经历过合并,比如从[a,b,c]合成[a,b,c,d,e],在这样的过程中,不论c的位置,在跟[d,e]合的时候在向右扩大并且在排序,去寻找小和,往右是一个不断扩大的过程。而往左,已经排序好了,一个合并好的数组是不会产生小和的,c只是普通的一员。类比成抓牌其实很容易理解。
逆序对问题
在一个数组中,左边的数如果比右边的数字大,则这两个数构成一个逆序对,请找到逆序对的数量。
与求小和问题一样,只是方向相反。
荷兰国旗问题
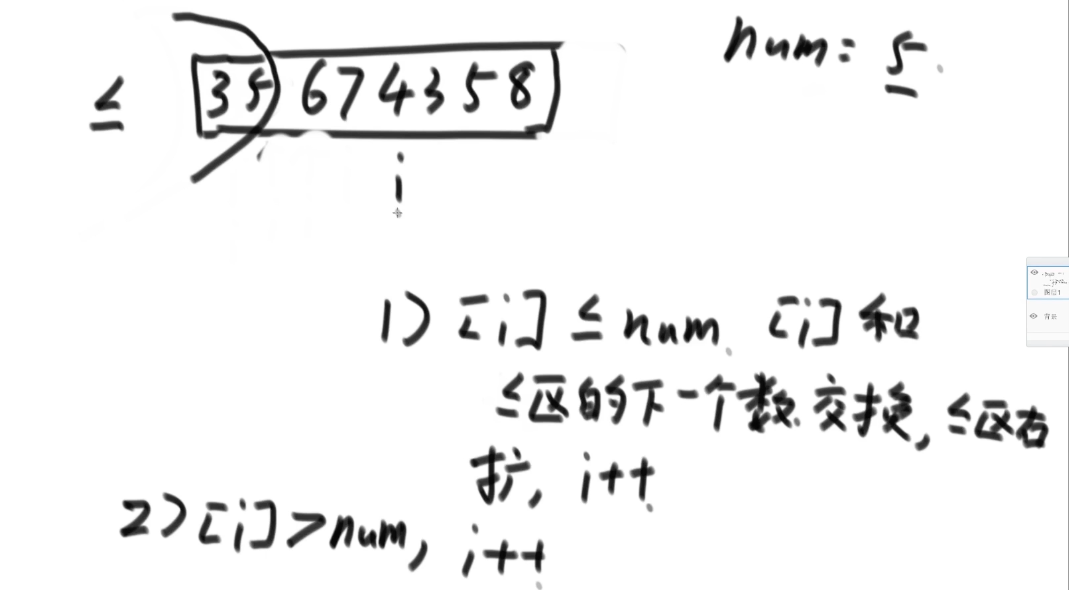
1.
给定一个数组arr,和一个数num,请把小于等于num的数放在数组的左边,大于num的数放在数组的右边,要求额外空间复杂度是O(1),时间复杂度O(N)。
没有要求左右两边有序。
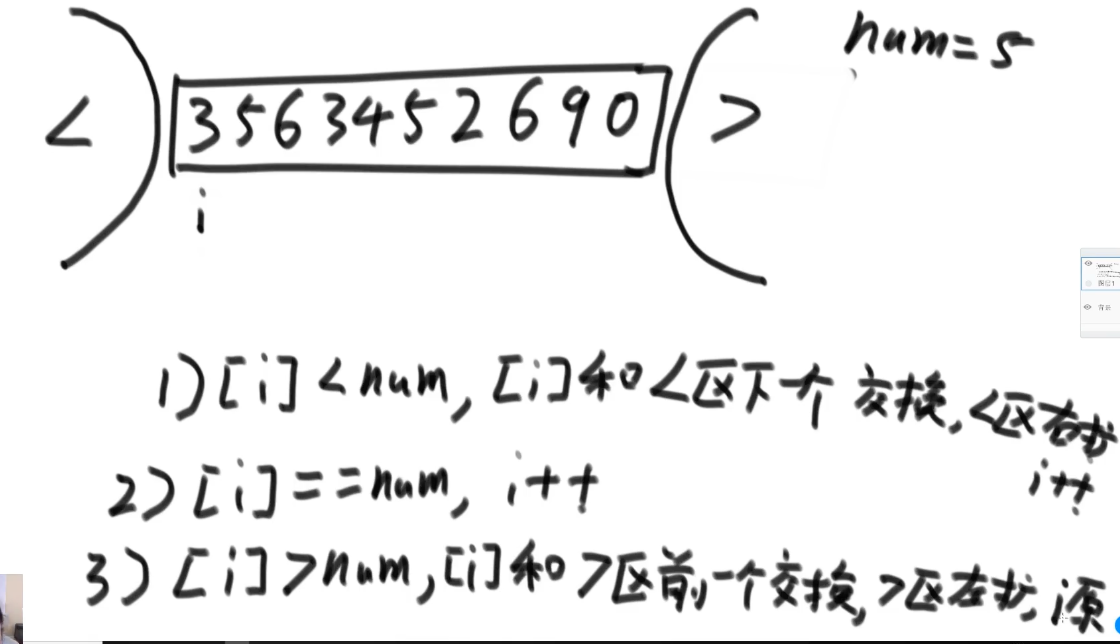
2.
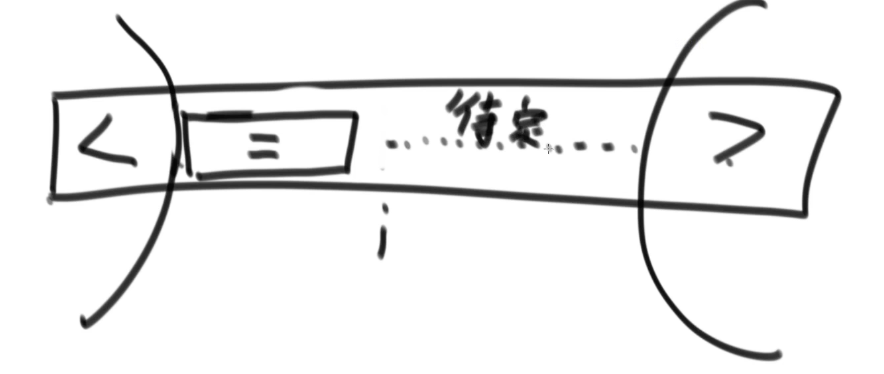
给定一个数组arr,和一个数num,请把小于等于num的数放在数组的左边,等于num的数放在数组的中间,大于num的数放在数组的右边,要求额外空间复杂度是O(1),时间复杂度O(N)。
第三个条件原地不动因为换过来了还没判断。
快排1.0
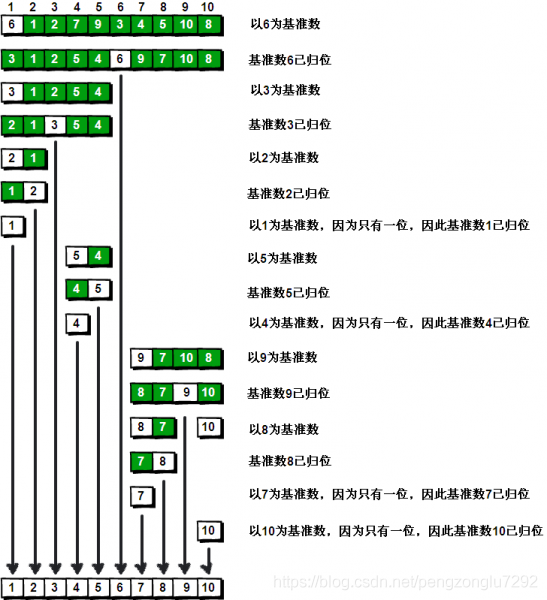
以下是来自曹利荣博客的内容
快速排序(过程图解)
快排2.0
2.0版本把基准数都放在中间,并且解决了一批基准数,然后两边再继续递归,实际上比1.0稍快一些。
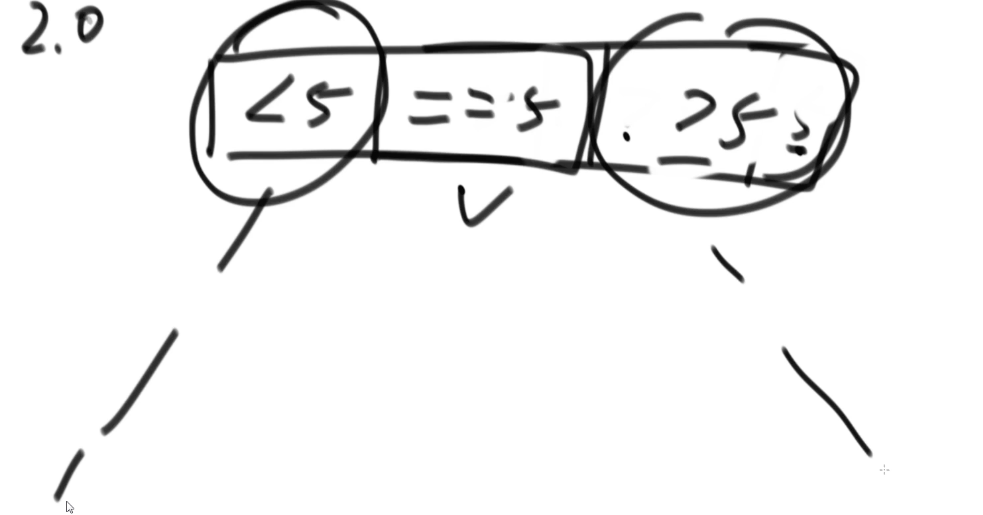
两个快排的时间复杂度都是,好情况是基准值几乎就在中间,这时候,即,差情况是基准值最左或最右。
快排3.0
即人为随机选一个数放到基准数,这样的话划分出来的位置好情况和坏情况就成了概率事件。最后的时间复杂度是
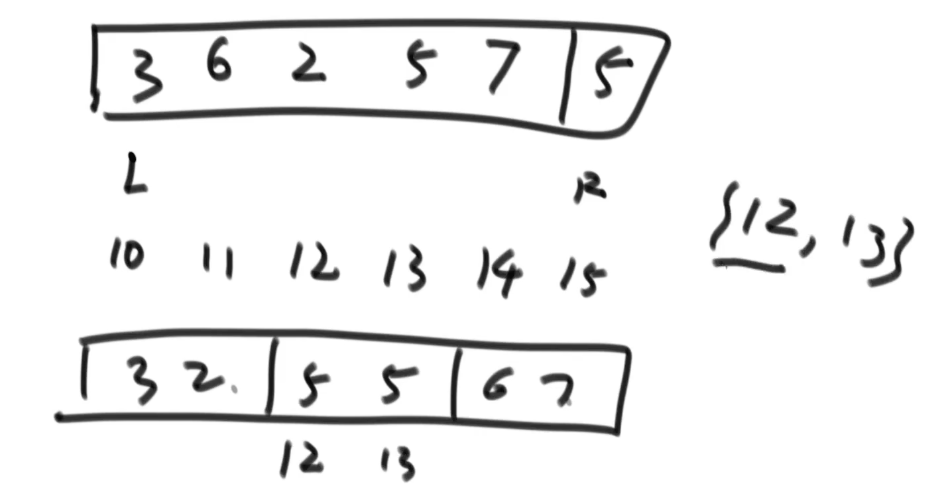
partition的过程就是将基准值5放到了中间,并且只返回两个数,即基准值等于区的左和右边界。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| public class Code06_QuickSort {
public static void quickSort(int[] arr){
if(arr == null || arr.length < 2){
return;
}
quickSort(arr , 0 , arr.length-1);
}
public static void quickSort(int[] arr , int L , int R){
if(L < R){
swap(arr , L + (int)(Math.random()*(R-L+1)),R);
int[] p = partition(arr , L , R);
quickSort(arr , L , p[0]-1);
quickSort(arr , p[1]+1 , R);
}
}
public static int[] partition(int[] arr , int L , int R) {
int less = L - 1;
int more = R;
while (L < more) {
if (arr[L] < arr[R]) {
swap(arr, ++less, L++);
} else if (arr[L] > arr[R]) {
swap(arr, --more, L);
} else {
L++;
}
}
swap(arr , more , R);
return new int[] {less + 1 , more };
}
public static void swap(int[] arr , int i , int j){
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
}
|
注意:
(int)(Math.random()*(R-L+1))
不要写成
(int)(Math.Random())*(R-L+1)。这样的结果一直为0.
快速排序的额外空间复杂度是,也是因为基准值的位置导致好情况和坏情况,与时间复杂度相似。